Применение динамических моделей при решении простейших тригонометрических уравнений
Решение любого тригонометрического уравнения в сводится к решению одного или нескольких простейших. Существует два способа решения простейших тригонометрических уравнений. Первый основан на применении готовых формул и требует очень хорошей памяти. Второй способ, логический и наглядный, основан на применении тригонометрического круга. Логика сильнее памяти, а потому второй путь решения тригонометрических уравнений надёжнее.
Алгоритм решения тригонометрических уравнений на круге прост и элегантен. Опишем его для уравнения cosx = a:
- на оси косинусов отложим число a;
- перпендикулярно оси косинусов проведем прямую до пересечения с окружностью;
- полученные точки запишем в ответ.
Как видим, алгоритм прост. Однако большие трудности возникают при изображении круга. К тому же в условиях дистанционного обучения это еще и значительные временные затраты. Эту проблему позволяет решить создание динамической модели для решения каждого из четырех видов простейших тригонометрических уравнений.
Модель для решения уравнения cosx=a выглядит так:
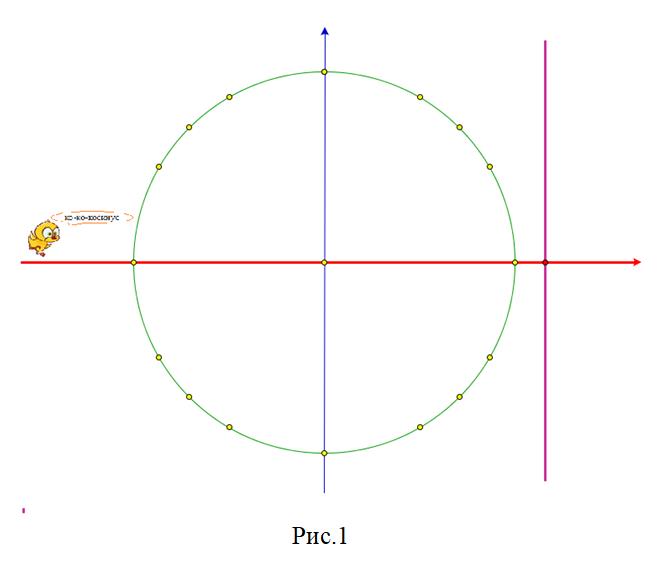
Красная точка на оси косинусов соответствует значению a. В данном случае (рис. 1) сиреневая прямая, перпендикулярная оси косинусов, окружность не пересекает, а потому уравнение решений не имеет.
Перемещая красную точку вдоль оси косинусов, будем получать решения уравнения cosx=a для разных значений a. В данном случае (рис. 2) сиреневая прямая, перпендикулярная оси косинусов, пересекает окружность дважды, а потому уравнение имеет две серии решений.
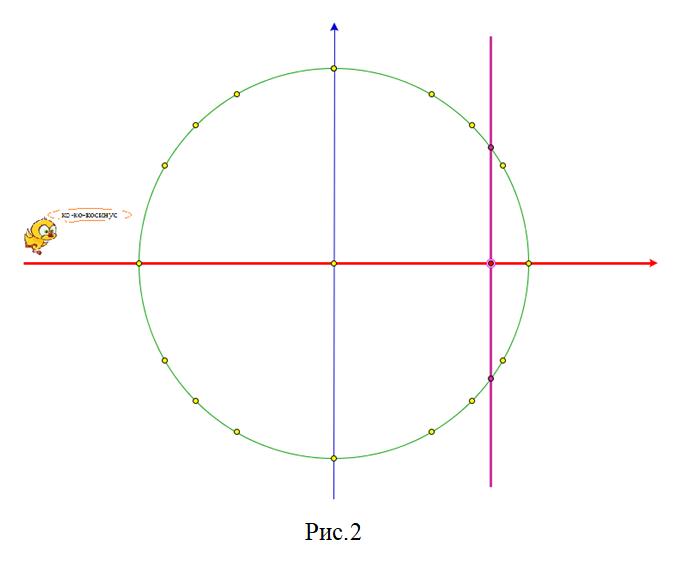
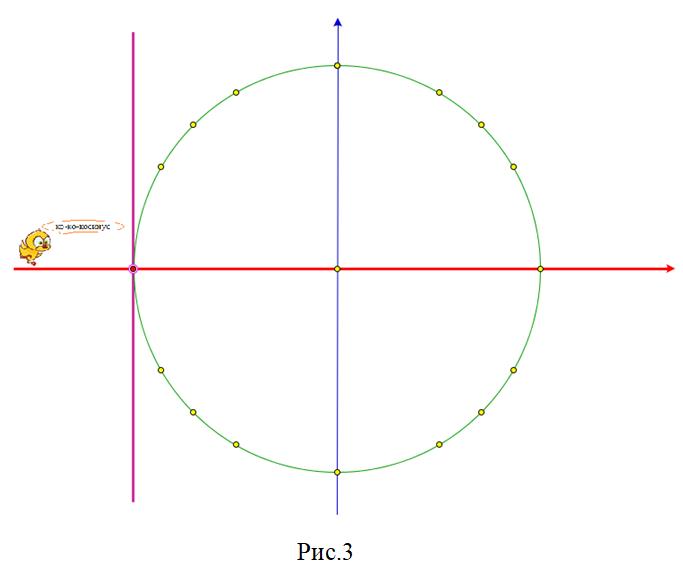
Рисунок 3 соответствует случаю, когда уравнение имеет одну серию корней.
Аналогичные динамические модели можно создать и для решения уравнений sinx = a, tgx = a, ctgx = a.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Великих Альфия Салиховна - педагог математики ДТ "Кванториум"
